也曾討論過，用 tree 來表示迷宮是一種頗為簡單、漂亮的作法。但是，從幾個產生的迷宮路徑圖來看（參考 8 月 15 日的 post），這種簡單方法所產生的迷宮「不夠蜿蜒曲折」。於是，就會想：如何才能產生比較蜿蜒曲折的迷宮呢？
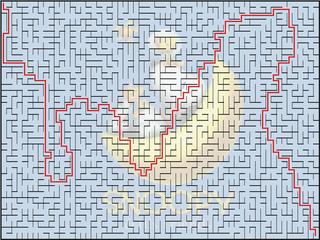
一種想法是，產生迷宮時（參考 8 月 25 日的 post），讓「候選集合 C」裡，每道「可被打破的牆」被打破的機率都不一樣。不過，問題是：該用怎樣的機率分配（該如何指定每道牆被選到、被打破的機率），才能得到蜿蜒的迷宮路徑呢？到目前為止，我試了幾種簡單的機率產生方式，但對結果都不甚滿意（有沒有人可以提供建議啊？）。換一個角度思考：我們可以觀察到，從左上到右下的路徑，必得經過中間每一直行。因此，或許可嘗試另一種方式：在迷宮中，隨意產生幾道「長長的、不可被打破的牆」，強迫從左上到右下的路徑必得「繞路」。例如，右上方的迷宮，第 10 行與第 26 行右側各有一道由上往下的長牆，第 14 行右側有一道由下往上的長牆。如此一來，產生的迷宮似乎就蜿蜒曲折了些。
我覺得，可以有「激發想法、並修改程式來實驗改進」的餘地，也是迷宮問題的有趣地方。
15 則留言:
這裡有很曲折的迷宮：（最新消息 (2004/1/13)）
高雄大學游森棚教授的網頁
這裡是我的解答，可以看出來他非常曲折
solution
嗯，真的是很曲折的迷宮呢。
很感謝「匿名者」的消息喔～
從匿名者所提供的這兩個連結裡，沒有找到產生這類迷宮的演算法 :(
雖然相信多花些力氣，應該可以從網路上取得更多資訊；但矛盾的是：沒有這麼多時間氣力？
建議多花點時間蒐集及過濾資料，如果覺得厭煩，就把在網路上搜尋當成玩 RPG就好了！
No pains, No gains!
基本上，我是覺得：能找到漂亮的演算法最好，但找不到也無妨。
換句話說，找到某種形式的答案，可以有「喔，原來如此」的感動；找不著，也可以有探索的樂趣。
而且，我想整理的這些東西，不是寫研究論文，而是從前樂趣的延續。以前不知道答案，現在也不見得就會知道。若是真找不著答案（例如各式的演算法），留給有興趣的讀者來動動腦，也是不錯。不是嗎？
喔，糟糕了，有人問到「蜿蜒的定義」囉。
事實上，我不知道該如何定義「蜿蜒」。不過，我覺得一般人，在看到路徑解答（例如，8/15 post 的路徑圖）時，似乎都可以「感覺」到它是否「頗為蜿蜒曲折」。
從「研究」的角度來說，有時定義反而是事後才加上去的。例如，假設 A, B 兩點間的最短距離是 x，而在迷宮中 A 至 B 的解答路徑距離為 y，我們或許可將「蜿蜒的程度」定義為 y - x。
當然啦，定義成這樣，好壞是很難說的。通常，我們會希望，定義與直觀是相契合的。
我第一個真正辛苦想過再寫出來的程式就是迷宮，記得是用Applesoft寫的。當初的寫法很笨，不過結果應該也是相當曲折，等有空寫再把結果貼上來。
喔，看來「迷宮」的確曾吸引過許多人的興趣。
很期待 MPH 可以提供一下他從前「曾辛苦想過」的方法，來交流一下。畢竟，曾經努力過的東西，不管最後是否成功（就像是我前些時候提到的，證明 Ackermann's function is not recursive），都會讓人印象深刻。
剛剛用 google 搜尋了一下，不過還是老問題「英文太差了」，實在很難抓到什麼重點，不過看起來好像用的就是那三種演算法產生，如果產生「稍微有些曲折的迷宮」，應該要花很多時間研究，不過下面這幾個網站蠻有趣的，還有程式可以玩一玩喔 :)
http://www.math.com/students/puzzles/mazegen/mazegen.html
http://www.billsgames.com/mazegenerator/
http://www.delphiforfun.org/Programs/maze.htm
嗯，還是貓對於網路搜尋資料比較在行 :)
第一個網址，連 Java source code 都有呢。看起來，它好像也是用 depth-first 的方式來產生迷宮的。
看了一下 MazeGen.java，應該有Prim及Kruskal方法的程式。
http://www.mazeworks.com/download/index.htm
case 0: mz = new MazeDFS(cp.getDim(),mc,cp,this) ; break ;
case 1: mz = new MazePrim(cp.getDim(),mc,cp,this) ; break ;
case 2: mz = new MazeKruskal(cp.getDim(),mc,cp,this) ; break ;
Prim 與 Kruskal 的演算法，應該是用來產生 minimum spanning tree 吧。
直觀上，depth-first search tree 所產生的迷宮，是以貪心法來增加從根節點到任意節點的最大距離；但 minimum spanning tree 所產生出來的迷宮，會有怎樣的（直觀）特性呢？
回想了一下之前的作法，好像和DFS沒什麼差別，不過當時什麼都不懂，不知道其實是這一回事罷了。
在單純的迷宮問題中節點間的權重全都一樣，所以所有的Spanning Tree都會是MST，不管用Prim或Kruskal結果都一樣。
如果照蜿蜒的字義把它定義為轉彎的路徑機率較大，不知道結果會如何？
嗯，我是該找時間，做個實驗嘗試看看...
張貼留言