年輕時,很容易手癢、想寫程式來解一些益智問題。
AB-game 也算是頗有趣的遊戲。因而,我在很久以前,就曾寫一支程式來(和使用者、或電腦自己)玩 AB-game。雖然那時自己其實對程式設計懂得很少,但最後還是能用 BASIC 語言,笨笨地、很暴力地 (ad hoc) 寫出「還算能夠玩」的程式。
回想起來,雖然頗覺得當時「不知天高地厚」,但心裏仍不免懷念那段年少輕狂的過去。也是因為最近試圖整理「從前感興趣的問題」,讓我回想起 AB-game。
從遊戲規則來看,要寫一支程式來檢查使用者的猜測,是相當容易的。程式可先依亂數選定一個數字,然後檢查使用者輸入的數字,回答幾 A 幾 B;直到使用者猜到程式所選的數字(回答 4A0B)為止。另一方面,要寫一支程式(扮演甲的角色來猜乙所選的數字),自動猜測使用者心裡所想的數字,似乎就不是那麼容易。
稍微分析一下,我們知道,在還沒有猜測前,乙選的數字有 10 x 9 x 8 x 7 = 5040 種可能。所以,即使乙並不需要回答幾 A 幾 B (僅需回答「是否猜中」),最糟的狀況下,我們也可以將這些可能的數字一個一個地拿來詢問「是這個數字嗎」,而在 5040 步內,猜中乙的答案。
而我們現在有乙所回答的「幾 A 幾 B」資訊,該如何利用它呢?最直接的方式,就是利用這項回答,從 5040 種可能(或者稱作「可能性空間」,possibilities space)裡,將不符合的數字刪掉。例如,如果猜測 1234 而得到回答 0A1B,那我們知道,答案不可能是 1234 (否則,回答應該是 4A0B)、不可能是 1567(若答案是 1567,猜 1234 的回答應為 1A0B)、也不可能是 8912 (回答會是 0A2B 而不是 0A1B)...。
因此,甲每猜測一次,就可以藉由乙的回答,從「可能性空間」裡,刪除一些「不可能是答案」的數字(也就是說,每一步都可以縮減可能性空間的大小)。於是,還保留在可能性空間裡的數字,就是「經過一連串猜測與回答後,仍有可能是答案」的那些數字。而我從前的程式,就是任意地從可能性空間中挑選出一個數字,來當作下個回合的猜測。
接下來的問題是:若演算法是任意由可能性空間裡,挑選一個數字,那麼最壞的情況下,需要猜測多少次呢?或者,更進一步:平均起來,需要猜幾次才能得到答案?還有:雖然可能性空間裡的數字,都有可能是答案;是否會有一些數字,它比其他的數字「更有可能」是答案?
雖然經過了這些年、似乎累積了更多電腦相關的知識;但我除了對從前的程式實作,有些改良的意見外,竟然也沒能想出更好的演算法與結果呢!
星期五, 9月 30, 2005
星期三, 9月 28, 2005
AB-game
雖然不知道 AB-game 的正式名稱,但我猜想,很多人都曾玩過類似的遊戲。
它是一種兩個人玩的遊戲:甲乙兩人各自在心裡想一個四位數字 (4 digits),然後輪流讓方猜測這個數字(而自己則對此猜測的數字,依下一段的說明做回應);能夠先猜出對方數字的人就算是贏家。
對於對方的猜測,回答的規則是這樣的:假設自己設想的數字是 a3a2a1a0(四位數字,在此千位數為 a3,百位數為 a2,十位數為 a1,個位數為 a0)而對方猜測的數字是 b3b2b1b0。若 x 為集合 {i | ai=ai} 的個數 (cardinality),而令 y 代表集合 {i | ai=bj, i ≠ j} 的個數,則我們的回答就是 xAyB。
換句話說,x 是「數字相同、位置也相同」的個數,y 是「數字相同、但位置不同」的個數。例如,若設想的數字是 1234,而對方猜測 3614,則我們回答 1A2B(數字 4 出現的位置相同;而數字 1、3 出現的位置不同);若設想的是 1357,對方猜 7890,則回答是 0A1B (沒有數字出現在相同的位置上;而有一個數字 7 出現在不同的位置)。
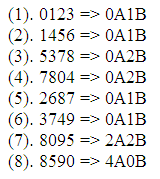 在 AB-game 裡,我們通常會要求猜想的四位數字不可重覆;也就是說,要求 ai≠aj (i ≠ j)。至於第一位(千位數)a3,一般則可以為零。因此,可猜想的數字,共有 10 x 9 x 8 x 7 = 5040 種可能。
在 AB-game 裡,我們通常會要求猜想的四位數字不可重覆;也就是說,要求 ai≠aj (i ≠ j)。至於第一位(千位數)a3,一般則可以為零。因此,可猜想的數字,共有 10 x 9 x 8 x 7 = 5040 種可能。
右圖是一個可能的猜測序列。乙所選定的數字為 8590,而甲的運氣不太好:他先猜 0123,得到回答 0A1B;接著猜 1456,又得到一樣的回答 0A1B;如此這般,甲總共花了八個步驟,才猜對 8590 這個數字。
花了這麼多篇幅介紹這個遊戲,我到底想說些什麼?
我想說的,是一段聽聞與經驗有些衝突,但沒有經過驗證 (prove or disprove) 的情事:印象中,似乎曾聽人說過,「最糟的狀況,也僅需猜六次」。然而,在我的記憶裡,雖然在大多數情況下,的確只需要猜六次,但我似乎也曾有要猜七次(或七次以上)的經驗。
所以,為什麼只需要猜六次,就可以得到答案呢?
它是一種兩個人玩的遊戲:甲乙兩人各自在心裡想一個四位數字 (4 digits),然後輪流讓方猜測這個數字(而自己則對此猜測的數字,依下一段的說明做回應);能夠先猜出對方數字的人就算是贏家。
對於對方的猜測,回答的規則是這樣的:假設自己設想的數字是 a3a2a1a0(四位數字,在此千位數為 a3,百位數為 a2,十位數為 a1,個位數為 a0)而對方猜測的數字是 b3b2b1b0。若 x 為集合 {i | ai=ai} 的個數 (cardinality),而令 y 代表集合 {i | ai=bj, i ≠ j} 的個數,則我們的回答就是 xAyB。
換句話說,x 是「數字相同、位置也相同」的個數,y 是「數字相同、但位置不同」的個數。例如,若設想的數字是 1234,而對方猜測 3614,則我們回答 1A2B(數字 4 出現的位置相同;而數字 1、3 出現的位置不同);若設想的是 1357,對方猜 7890,則回答是 0A1B (沒有數字出現在相同的位置上;而有一個數字 7 出現在不同的位置)。
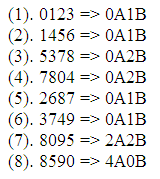 在 AB-game 裡,我們通常會要求猜想的四位數字不可重覆;也就是說,要求 ai≠aj (i ≠ j)。至於第一位(千位數)a3,一般則可以為零。因此,可猜想的數字,共有 10 x 9 x 8 x 7 = 5040 種可能。
在 AB-game 裡,我們通常會要求猜想的四位數字不可重覆;也就是說,要求 ai≠aj (i ≠ j)。至於第一位(千位數)a3,一般則可以為零。因此,可猜想的數字,共有 10 x 9 x 8 x 7 = 5040 種可能。右圖是一個可能的猜測序列。乙所選定的數字為 8590,而甲的運氣不太好:他先猜 0123,得到回答 0A1B;接著猜 1456,又得到一樣的回答 0A1B;如此這般,甲總共花了八個步驟,才猜對 8590 這個數字。
花了這麼多篇幅介紹這個遊戲,我到底想說些什麼?
我想說的,是一段聽聞與經驗有些衝突,但沒有經過驗證 (prove or disprove) 的情事:印象中,似乎曾聽人說過,「最糟的狀況,也僅需猜六次」。然而,在我的記憶裡,雖然在大多數情況下,的確只需要猜六次,但我似乎也曾有要猜七次(或七次以上)的經驗。
所以,為什麼只需要猜六次,就可以得到答案呢?
星期六, 9月 24, 2005
簡報後的檢討
昨天簡報後,自己總覺得不太對勁。
問題出在哪兒呢?我想了想,大致上或可說是:「準備不足、時間不夠、缺乏互動」。
首先,是遇到螢幕大小的問題。由於先前沒有使用「寬螢幕筆記型電腦」的經驗,不知道接上投影機後,會產生字體扭曲的現象。事後,我猜測是(筆電螢幕與投影機螢幕)解析度不同的緣故;但自己也頗好奇,為什麼產品手冊上,沒有教使用者如何處理這類狀況?
說來也真奇怪,我這回買的 HP Presario B1800 筆電,竟然沒有附產品的說明或使用手冊。大概是 HP 以為使用者都知道鍵盤上各式按鍵的使用方式、也都瞭解各類燈號的意義。可是,我就曾經因為不知道有個「打開無線網路」的按鈕而虛耗數個小時呢(參看 8 月 31 日的 post)。現在,自己碰到「螢幕解析度」的問題後,不免會想:「難道,只有我才會碰到這種狀況;只有我才會認為:它是個需被解決的問題?」
我猜測這個問題,與多重螢幕的設定有關;不過自己並不瞭解多重螢幕間,設定、切換、與運作的方式。有沒有人(喂,萬事通的貓啊,快幫我想想辦法吧)能夠提供合適的建議或解答呢?(還是,乾脆該打電話向廠商求教?)
除了「簡報顯示扭曲、自己與觀眾看了都不順眼」之外,我覺得「投影片準備不足、簡報時間不夠」也是項缺點。說投影片準備得不足,其實該說是自己並沒有想清楚:這次的簡報,究竟想達成些什麼。而簡報的時間不足,除了頭頭(項老師)有事必須提前離開;簡報期間太太數次行動電話 call-in ,也讓自己顯得手忙腳亂。
最後,關於缺乏互動的部分,自己似乎早該知道、也該事先有所準備(如此就不會對「缺乏互動」感到不安)。在做簡報前,已經有三位學弟報告過了。輪番上陣、疲勞轟炸的結果,聽眾早已心力交瘁、頭昏眼花,怎能有氣力與意願,來做良好的溝通與互動呢?
問題出在哪兒呢?我想了想,大致上或可說是:「準備不足、時間不夠、缺乏互動」。
首先,是遇到螢幕大小的問題。由於先前沒有使用「寬螢幕筆記型電腦」的經驗,不知道接上投影機後,會產生字體扭曲的現象。事後,我猜測是(筆電螢幕與投影機螢幕)解析度不同的緣故;但自己也頗好奇,為什麼產品手冊上,沒有教使用者如何處理這類狀況?
說來也真奇怪,我這回買的 HP Presario B1800 筆電,竟然沒有附產品的說明或使用手冊。大概是 HP 以為使用者都知道鍵盤上各式按鍵的使用方式、也都瞭解各類燈號的意義。可是,我就曾經因為不知道有個「打開無線網路」的按鈕而虛耗數個小時呢(參看 8 月 31 日的 post)。現在,自己碰到「螢幕解析度」的問題後,不免會想:「難道,只有我才會碰到這種狀況;只有我才會認為:它是個需被解決的問題?」
我猜測這個問題,與多重螢幕的設定有關;不過自己並不瞭解多重螢幕間,設定、切換、與運作的方式。有沒有人(喂,萬事通的貓啊,快幫我想想辦法吧)能夠提供合適的建議或解答呢?(還是,乾脆該打電話向廠商求教?)
除了「簡報顯示扭曲、自己與觀眾看了都不順眼」之外,我覺得「投影片準備不足、簡報時間不夠」也是項缺點。說投影片準備得不足,其實該說是自己並沒有想清楚:這次的簡報,究竟想達成些什麼。而簡報的時間不足,除了頭頭(項老師)有事必須提前離開;簡報期間太太數次行動電話 call-in ,也讓自己顯得手忙腳亂。
最後,關於缺乏互動的部分,自己似乎早該知道、也該事先有所準備(如此就不會對「缺乏互動」感到不安)。在做簡報前,已經有三位學弟報告過了。輪番上陣、疲勞轟炸的結果,聽眾早已心力交瘁、頭昏眼花,怎能有氣力與意願,來做良好的溝通與互動呢?
星期五, 9月 23, 2005
回實驗室給了一場簡短報告
準備了一個多星期,今天下午在實驗室給了場簡短的報告。
報告的內容,就像是上星期五所提到的,是嘗試以「見樹」的方式、換個角度看待古契書文件群。因此,雖然自己對古契書其實一點都不懂,還是努力假想了一個使用情境,然後從中看看是否能夠學習到什麼。
或許是時間不夠、或許是很久沒有在學校做過簡報,又或許是自己準備得還不夠,我總覺得許多地方講得不是很好(也就是說,詞不達意、講得不清楚啦)。不過,除了自己可以學習簡報技巧外,我還是傾向於將簡報看作「報告者與聽眾的溝通與交流」;聽眾(學弟妹們)的感受、收穫、想法與回饋,才是最實際、也最重要的。
報告的內容,就像是上星期五所提到的,是嘗試以「見樹」的方式、換個角度看待古契書文件群。因此,雖然自己對古契書其實一點都不懂,還是努力假想了一個使用情境,然後從中看看是否能夠學習到什麼。
或許是時間不夠、或許是很久沒有在學校做過簡報,又或許是自己準備得還不夠,我總覺得許多地方講得不是很好(也就是說,詞不達意、講得不清楚啦)。不過,除了自己可以學習簡報技巧外,我還是傾向於將簡報看作「報告者與聽眾的溝通與交流」;聽眾(學弟妹們)的感受、收穫、想法與回饋,才是最實際、也最重要的。
星期四, 9月 22, 2005
科教館的玩具
如果有用心,在台北常能發現有趣的事物。
 例如,士林有一座國立科學教育館,假日人潮洶湧,但上班日通常門可羅雀,非常適合帶小朋友去走走。更棒的是,即使不買門票,也常能得到許多樂趣。
例如,士林有一座國立科學教育館,假日人潮洶湧,但上班日通常門可羅雀,非常適合帶小朋友去走走。更棒的是,即使不買門票,也常能得到許多樂趣。
我們因為常有事到士林,偶而也會帶寶寶到那兒,看看門外的「球球坐電梯」。它是一座很有趣的機器,利用傳輸帶將球帶到高處,然後讓它由高處滾動滑下、撞擊、彈跳(右圖是這座機器的部分展示 -- Blogger 似乎會把上載的動態圖弄壞)。不僅很多小朋友喜歡駐足觀賞,我也常常在那兒感到歡欣讚嘆。
該館一、二樓有賣許多玩具,也提供一些樣本讓小朋友試玩。非假日期間,寶寶通常都能玩得頗愉快。有時,也可以找到一些有趣的益智遊戲,讓大人們也都能玩上好一陣子。
昨天帶三歲的寶寶去科教館,又發現一個可愛的玩具。它其實是一隻氣球,但日本人發揮巧思,在氣球下裝上合適重量的膠紙(作為動物的腳),讓氣球漂浮在離地約 10 公分處。小傢伙用線牽著氣球走,就像是牽著真實的動物一樣可愛。
雖然價格有些偏高,但寶寶玩得高興、又覺得需要鼓勵這類的創意,我決定讓她自己挑一隻。連問數次,小傢伙都選了「小公雞」。我讓她牽著小公雞在館內四處逛、教她到二樓書局講故事給小公雞聽 -- 而或許是因為看到寶寶高興的樣子,我在那些時刻裡,確實感覺頗為幸福。
下圖就是這隻「小公雞氣球」的長相。遠遠看來,還頗像真的公雞呢。

 例如,士林有一座國立科學教育館,假日人潮洶湧,但上班日通常門可羅雀,非常適合帶小朋友去走走。更棒的是,即使不買門票,也常能得到許多樂趣。
例如,士林有一座國立科學教育館,假日人潮洶湧,但上班日通常門可羅雀,非常適合帶小朋友去走走。更棒的是,即使不買門票,也常能得到許多樂趣。我們因為常有事到士林,偶而也會帶寶寶到那兒,看看門外的「球球坐電梯」。它是一座很有趣的機器,利用傳輸帶將球帶到高處,然後讓它由高處滾動滑下、撞擊、彈跳(右圖是這座機器的部分展示 -- Blogger 似乎會把上載的動態圖弄壞)。不僅很多小朋友喜歡駐足觀賞,我也常常在那兒感到歡欣讚嘆。
該館一、二樓有賣許多玩具,也提供一些樣本讓小朋友試玩。非假日期間,寶寶通常都能玩得頗愉快。有時,也可以找到一些有趣的益智遊戲,讓大人們也都能玩上好一陣子。
昨天帶三歲的寶寶去科教館,又發現一個可愛的玩具。它其實是一隻氣球,但日本人發揮巧思,在氣球下裝上合適重量的膠紙(作為動物的腳),讓氣球漂浮在離地約 10 公分處。小傢伙用線牽著氣球走,就像是牽著真實的動物一樣可愛。
雖然價格有些偏高,但寶寶玩得高興、又覺得需要鼓勵這類的創意,我決定讓她自己挑一隻。連問數次,小傢伙都選了「小公雞」。我讓她牽著小公雞在館內四處逛、教她到二樓書局講故事給小公雞聽 -- 而或許是因為看到寶寶高興的樣子,我在那些時刻裡,確實感覺頗為幸福。
下圖就是這隻「小公雞氣球」的長相。遠遠看來,還頗像真的公雞呢。

星期一, 9月 19, 2005
AI 是什麼?
上星期五實驗室聚餐,項老師也出席了。
席間,老師半開玩笑似地說,AI(Artificial Intelligence,人工智能,從前翻譯為人工智慧)是一個很奇怪的領域。他說,AI 有許多定義,其中的一個定義是:「AI 是研究那些人腦可以做,而電腦卻不能做的事情」。
依照這個定義,老師說,AI 裡研究的主題,一旦成熟後,就會獨立出個別的學門,不再算是 AI 了。例如,幾個從前被認為算是 AI 領域的學科,像是 Image Processing(影像處理)、Theorem Proving (定理證明)、Robotics(機器人學)等,在漸漸成熟、知道如何運算出夠好的結果後,都獨立出自己的學門;而研究這些主題的學者,也都不再認為自己 是在做 AI 的研究了。
老師接著說,「所以,AI 存在的目的,就是為了消滅它自己,那真是怪異 (weird) 啊。」
其實,項老師在十年前,就講過一樣的話了。但從現實面看,就算我們真的是如此定義 AI,而 AI 的存在,也真的只是為了消滅它自己,那又如何呢?
即使最終電腦可以取代人腦,但 AI 身為衍生出這些有價值的獨立學門之母,應也足夠了,不是嗎?更何況,我是屬於「認為電腦無法取代人腦」的人;而只要存在某些事情,是人腦做得比電腦好的,那 AI 也就有存在的價值啊。
後記:由此也可看出,學數學的人(項老師)對「定義」的敏銳程度。學工程的人或許會覺得,定義沒有弄得很清楚也不打緊,系統做得出來、運作無誤就好了。但做科學研究、尤其是有志於理論研究者,似乎還是該先瞭解定義比較好。
席間,老師半開玩笑似地說,AI(Artificial Intelligence,人工智能,從前翻譯為人工智慧)是一個很奇怪的領域。他說,AI 有許多定義,其中的一個定義是:「AI 是研究那些人腦可以做,而電腦卻不能做的事情」。
依照這個定義,老師說,AI 裡研究的主題,一旦成熟後,就會獨立出個別的學門,不再算是 AI 了。例如,幾個從前被認為算是 AI 領域的學科,像是 Image Processing(影像處理)、Theorem Proving (定理證明)、Robotics(機器人學)等,在漸漸成熟、知道如何運算出夠好的結果後,都獨立出自己的學門;而研究這些主題的學者,也都不再認為自己 是在做 AI 的研究了。
老師接著說,「所以,AI 存在的目的,就是為了消滅它自己,那真是怪異 (weird) 啊。」
其實,項老師在十年前,就講過一樣的話了。但從現實面看,就算我們真的是如此定義 AI,而 AI 的存在,也真的只是為了消滅它自己,那又如何呢?
即使最終電腦可以取代人腦,但 AI 身為衍生出這些有價值的獨立學門之母,應也足夠了,不是嗎?更何況,我是屬於「認為電腦無法取代人腦」的人;而只要存在某些事情,是人腦做得比電腦好的,那 AI 也就有存在的價值啊。
後記:由此也可看出,學數學的人(項老師)對「定義」的敏銳程度。學工程的人或許會覺得,定義沒有弄得很清楚也不打緊,系統做得出來、運作無誤就好了。但做科學研究、尤其是有志於理論研究者,似乎還是該先瞭解定義比較好。
星期五, 9月 16, 2005
即使不必上班,日子依舊忙碌
又過了兩個不必上班的星期。
這十幾天來,做了些什麼事情呢?星期一、三、五陪同太太帶寶寶出門,星期二、四在家裡陪寶寶。雖說陪寶寶玩樂、看著寶寶長大,也經常會得到強烈的幸福感,不過一旦想起「還有許多待做的事情未做」、「還有許多想看的書未看」,就會滿心愧疚。
還好,利用早上大家還在睡覺的時間,自己倒也是做了許多事情。除了寫幾篇 Blogs、嘗試著修改程式,讓迷宮更為曲折外,還有些「登不上台面」、但卻也重要的瑣事。例如,檢視前些日子從學弟妹們那裡取得的「古契書」文字檔。
雖然不甚確定,但我覺得「如何檢索這些古契書」,是項老師與學弟妹們這幾年來做「數位圖書館」研究的一個重要項目。自己的博士論文,研究的就是關於資訊檢索 (information retrieval) 的主題,所以或可提供一些自己的經驗或心得,讓學弟妹們少走些冤枉路。
聽過兩次學弟們的報告,我猜測大家對於使用 general-purposed approaches 應該已經有了相當程度的瞭解,但或許對比較特定的應用缺乏感覺。也就是說,大家看讀過、也實驗過「同時處理多篇文件」的方式(例如,利用統計方法來斷詞),但卻可能會有「見林不見樹」的遺憾(在此,每一篇文件是樹,而整個文件集合 (corpus) 就是林)。
因此,我想採取「見樹」(the small) 的方式,從比較特定的一些文件著手,看看是否能激發學弟妹們的一些想像(以公司裡使用的詞彙來說,就是「創意」)。當然啦,要「見樹」,自然得對「樹」有相當程度的瞭解;但不幸的是:我對古契書的背景與文字內容,瞭解非常貧乏(似乎也只有歷史學者才會比較瞭解 -- 但不該以此作為藉口)。因此,很可能自己花了不少氣力描繪出來的「樹」,與實際上的「樹」會有著相當大的落差。
我想,做研究就是這樣,總是得嘗試去做些「雖然辛苦、也不知是否會豐收」的事情;而這也是「做研究」與「產品開發」的一個主要不同處吧。
這十幾天來,做了些什麼事情呢?星期一、三、五陪同太太帶寶寶出門,星期二、四在家裡陪寶寶。雖說陪寶寶玩樂、看著寶寶長大,也經常會得到強烈的幸福感,不過一旦想起「還有許多待做的事情未做」、「還有許多想看的書未看」,就會滿心愧疚。
還好,利用早上大家還在睡覺的時間,自己倒也是做了許多事情。除了寫幾篇 Blogs、嘗試著修改程式,讓迷宮更為曲折外,還有些「登不上台面」、但卻也重要的瑣事。例如,檢視前些日子從學弟妹們那裡取得的「古契書」文字檔。
雖然不甚確定,但我覺得「如何檢索這些古契書」,是項老師與學弟妹們這幾年來做「數位圖書館」研究的一個重要項目。自己的博士論文,研究的就是關於資訊檢索 (information retrieval) 的主題,所以或可提供一些自己的經驗或心得,讓學弟妹們少走些冤枉路。
聽過兩次學弟們的報告,我猜測大家對於使用 general-purposed approaches 應該已經有了相當程度的瞭解,但或許對比較特定的應用缺乏感覺。也就是說,大家看讀過、也實驗過「同時處理多篇文件」的方式(例如,利用統計方法來斷詞),但卻可能會有「見林不見樹」的遺憾(在此,每一篇文件是樹,而整個文件集合 (corpus) 就是林)。
因此,我想採取「見樹」(the small) 的方式,從比較特定的一些文件著手,看看是否能激發學弟妹們的一些想像(以公司裡使用的詞彙來說,就是「創意」)。當然啦,要「見樹」,自然得對「樹」有相當程度的瞭解;但不幸的是:我對古契書的背景與文字內容,瞭解非常貧乏(似乎也只有歷史學者才會比較瞭解 -- 但不該以此作為藉口)。因此,很可能自己花了不少氣力描繪出來的「樹」,與實際上的「樹」會有著相當大的落差。
我想,做研究就是這樣,總是得嘗試去做些「雖然辛苦、也不知是否會豐收」的事情;而這也是「做研究」與「產品開發」的一個主要不同處吧。
星期二, 9月 13, 2005
更為曲折的迷宮
在「稍微有些曲折的迷宮」貼出後,MPH 提出「曲折」的建議:盡量讓迷宮多轉些彎。
 說的也是。既然手頭有程式,當然應該試著修改參數、做些實驗,看看會有怎樣不同的結果?
說的也是。既然手頭有程式,當然應該試著修改參數、做些實驗,看看會有怎樣不同的結果?
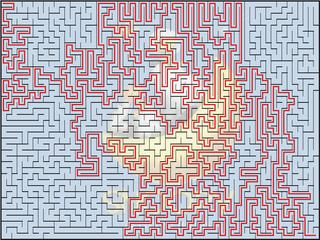
回想一下,我們的演算法,是採用 depth-first search (DFS) 的方式來展開迷宮樹狀結構的。原先的程式,在選擇「欲打破的牆」時,並沒有加入「盡量多轉彎」的考量。現在,我們讓迷宮路徑會轉彎的機率,比直線走的機率高。
例如,假設轉彎的機率是走直線的兩倍。再假設我們現在處於節點 (2,4),且發現其左側牆已被打通。則可知道,我們是站在節點 (2,4) 上,面向右(因為剛剛是由 (2,3) 走過來的)。於是,我們就讓 (2,4) 節點上方與下方(分別表示「左轉」與「右轉」)的牆,被打破的機率,是右側(表示「走直線」)牆的兩倍。
而這回產生的迷宮,看起來又更曲折了(參考右上方圖例,並與先前的迷宮做比較)。
這給了我們一個經驗:在定義「蜿蜒曲折」時,似乎不僅僅可「拉長兩端點間的距離」,也該考慮「轉彎的次數」!
喔,這下麻煩大了。原本「蜿蜒曲折」就是一個「未經明確定義」的詞彙;但現在它的意義,變得更複雜(拉長、多彎)後,會不會讓討論變得更模糊呢?
而且,也還有一些或許更困難、更有趣的後續討論哩。現在我們已經有了「感覺起來」頗為曲折的迷宮;但是「好」迷宮,光是蜿蜒曲折,應該還是不夠的。我們並不希望:迷宮蜿蜒曲折,但是「很好走」(例如,從入口到出口,幾乎都沒有岔路;或者,就算迷宮有很多岔路,但岔路都很短,一下就走到岔路盡頭)。
所以,接下來該怎麼延續「迷宮」的研究、討論、與實驗呢?
 說的也是。既然手頭有程式,當然應該試著修改參數、做些實驗,看看會有怎樣不同的結果?
說的也是。既然手頭有程式,當然應該試著修改參數、做些實驗,看看會有怎樣不同的結果?回想一下,我們的演算法,是採用 depth-first search (DFS) 的方式來展開迷宮樹狀結構的。原先的程式,在選擇「欲打破的牆」時,並沒有加入「盡量多轉彎」的考量。現在,我們讓迷宮路徑會轉彎的機率,比直線走的機率高。
例如,假設轉彎的機率是走直線的兩倍。再假設我們現在處於節點 (2,4),且發現其左側牆已被打通。則可知道,我們是站在節點 (2,4) 上,面向右(因為剛剛是由 (2,3) 走過來的)。於是,我們就讓 (2,4) 節點上方與下方(分別表示「左轉」與「右轉」)的牆,被打破的機率,是右側(表示「走直線」)牆的兩倍。
而這回產生的迷宮,看起來又更曲折了(參考右上方圖例,並與先前的迷宮做比較)。
這給了我們一個經驗:在定義「蜿蜒曲折」時,似乎不僅僅可「拉長兩端點間的距離」,也該考慮「轉彎的次數」!
喔,這下麻煩大了。原本「蜿蜒曲折」就是一個「未經明確定義」的詞彙;但現在它的意義,變得更複雜(拉長、多彎)後,會不會讓討論變得更模糊呢?
而且,也還有一些或許更困難、更有趣的後續討論哩。現在我們已經有了「感覺起來」頗為曲折的迷宮;但是「好」迷宮,光是蜿蜒曲折,應該還是不夠的。我們並不希望:迷宮蜿蜒曲折,但是「很好走」(例如,從入口到出口,幾乎都沒有岔路;或者,就算迷宮有很多岔路,但岔路都很短,一下就走到岔路盡頭)。
所以,接下來該怎麼延續「迷宮」的研究、討論、與實驗呢?
星期日, 9月 11, 2005
能夠「輸出自己」的程式
前些日子提到 Ackermann's function 後,也讓我回想起一些有趣的小問題。
其中一個,是寫個程式,它不管輸入什麼,都會輸出自己(這份程式)。這個問題之所以有趣,一部份的原因,是因為乍看之下,要求得一組解(寫出一個能夠「輸出自己」的程式),似乎並不困難。但真的如此容易嗎?有興趣的人可以試試看。
第一次碰到這個問題,也是在 Maryland 時,計算理論老師 (Dr. Smith) 的講義裡,某個習題提到的。當時是沒有出這項作業,但我有花幾個小時嘗試寫過,並沒有成功。(嗯,還是一樣,沒有成功解出的問題,比較會印象深刻...)
在課堂上,老師也提到過,我們可以證明:不管是哪種程式語言 (只要它們的計算能力相同,都是 Turing-complete -- 現在幾乎所有的程式語言,像是 C、BASIC、JAVA、LISP、PASCAL、PROLOG,甚至 PHP,都是 Turing-complete),總是存在著(無限多個)這樣的程式,它們可以輸出「它們自己」(此證明可參考這本書末,對習題 2.13 的解答)。
自己則是在數年後,從 BBS 上看到有人貼出用 C 語言實作的漂亮答案。我將它稍微修改,展現成 PHP 的程式碼:
<?php $s='<?php $s=%c%s%c;printf($s,39,$s,39); ?>';printf($s,39,$s,39); ?>
你能夠自己寫出這樣的程式嗎?
其中一個,是寫個程式,它不管輸入什麼,都會輸出自己(這份程式)。這個問題之所以有趣,一部份的原因,是因為乍看之下,要求得一組解(寫出一個能夠「輸出自己」的程式),似乎並不困難。但真的如此容易嗎?有興趣的人可以試試看。
第一次碰到這個問題,也是在 Maryland 時,計算理論老師 (Dr. Smith) 的講義裡,某個習題提到的。當時是沒有出這項作業,但我有花幾個小時嘗試寫過,並沒有成功。(嗯,還是一樣,沒有成功解出的問題,比較會印象深刻...)
在課堂上,老師也提到過,我們可以證明:不管是哪種程式語言 (只要它們的計算能力相同,都是 Turing-complete -- 現在幾乎所有的程式語言,像是 C、BASIC、JAVA、LISP、PASCAL、PROLOG,甚至 PHP,都是 Turing-complete),總是存在著(無限多個)這樣的程式,它們可以輸出「它們自己」(此證明可參考這本書末,對習題 2.13 的解答)。
自己則是在數年後,從 BBS 上看到有人貼出用 C 語言實作的漂亮答案。我將它稍微修改,展現成 PHP 的程式碼:
<?php $s='<?php $s=%c%s%c;printf($s,39,$s,39); ?>';printf($s,39,$s,39); ?>
你能夠自己寫出這樣的程式嗎?
星期三, 9月 07, 2005
「稍微曲折的迷宮」之後
頗訝異於網路的高效率。
昨天貼出「稍微曲折的迷宮」後,不到半天就有人回應,說這裡有張曲折的迷宮圖,而這裡是它的路徑解答。
喔, 那可是張很大 (3002x3002) 的迷宮圖呢。很可惜,我沒有找到產生這張迷宮的演算法(與程式)。不過,有時直接看到答案,雖然會有「啊哈,原來如此」的痛快,但緊接著可能就會有些莫名 的失落。找不著答案,我們可以試著修改自己的演算法,想想如何才能產生蜿蜒曲折的迷宮。而探索,不也是一種樂趣嗎?
 昨晚花了些時間,修改程式來做些實驗。終於,我們可以產生像右圖般的迷宮了。它看起來比昨天的迷宮,就蜿蜒曲折了許多(雖然我們也還是沒有定義出什麼叫做「蜿蜒曲折」)。
昨晚花了些時間,修改程式來做些實驗。終於,我們可以產生像右圖般的迷宮了。它看起來比昨天的迷宮,就蜿蜒曲折了許多(雖然我們也還是沒有定義出什麼叫做「蜿蜒曲折」)。
這個迷宮是如何被產生的呢?
回顧之前提過的一個想法:或許可藉由增加迷宮的直徑(diameter,就是最長的兩端點距離)來產生曲折的迷宮。但是,要用什麼方式來怎樣增加迷宮的直徑,才能夠依然保持演算法的簡潔呢?
一個「也算直觀」的想法,是在產生迷宮的樹狀圖(8 月 25 日 post 的集合 T)時,儘量增加 T 的高度(height,由根節點到任意節點的最長距離)。也就是說,每當我們從集合 C 裡,要選出「可被打破的牆」時,儘量選「能夠繼續增長迷宮樹狀圖高度」的牆來打破。
最簡單的一種方式,是當我們要將節點四周「可被打破的牆」放入集合 C 時(參考 8 月 25 日 post 的步驟 2),實際上只選一面牆放入集合 C (其他的幾面牆,則放入另一個串列 C2)。如此一來,我們可以讓 T 以類似深度優先 (depth-first) 搜尋的方式向外延伸,而能夠相對容易地增加 T 的高度。
那麼,如果 T 已經「碰到絕處」,無法用深度優先搜尋繼續往下增長時,該怎麼辦呢?此時,我們可以由 C2 取出最後面的牆來打破。如此持續進行,直到 C 與 C2 都是空集合為止。(喔,只是稍微修改 8 月 25 日 post 的「基本演算法」,產生出來的結果,竟然就會有如此大的差異...)
我想,或許迷宮真的是一個不錯的主題吧(連 MPH 從前也曾嘗試用「笨方法」產生曲折迷宮呢)。而回顧這些曾感興趣的問題,總讓我對從前懵懂的歲月,有著淡淡的感傷、歡喜與寂寞。
昨天貼出「稍微曲折的迷宮」後,不到半天就有人回應,說這裡有張曲折的迷宮圖,而這裡是它的路徑解答。
喔, 那可是張很大 (3002x3002) 的迷宮圖呢。很可惜,我沒有找到產生這張迷宮的演算法(與程式)。不過,有時直接看到答案,雖然會有「啊哈,原來如此」的痛快,但緊接著可能就會有些莫名 的失落。找不著答案,我們可以試著修改自己的演算法,想想如何才能產生蜿蜒曲折的迷宮。而探索,不也是一種樂趣嗎?
 昨晚花了些時間,修改程式來做些實驗。終於,我們可以產生像右圖般的迷宮了。它看起來比昨天的迷宮,就蜿蜒曲折了許多(雖然我們也還是沒有定義出什麼叫做「蜿蜒曲折」)。
昨晚花了些時間,修改程式來做些實驗。終於,我們可以產生像右圖般的迷宮了。它看起來比昨天的迷宮,就蜿蜒曲折了許多(雖然我們也還是沒有定義出什麼叫做「蜿蜒曲折」)。這個迷宮是如何被產生的呢?
回顧之前提過的一個想法:或許可藉由增加迷宮的直徑(diameter,就是最長的兩端點距離)來產生曲折的迷宮。但是,要用什麼方式來怎樣增加迷宮的直徑,才能夠依然保持演算法的簡潔呢?
一個「也算直觀」的想法,是在產生迷宮的樹狀圖(8 月 25 日 post 的集合 T)時,儘量增加 T 的高度(height,由根節點到任意節點的最長距離)。也就是說,每當我們從集合 C 裡,要選出「可被打破的牆」時,儘量選「能夠繼續增長迷宮樹狀圖高度」的牆來打破。
最簡單的一種方式,是當我們要將節點四周「可被打破的牆」放入集合 C 時(參考 8 月 25 日 post 的步驟 2),實際上只選一面牆放入集合 C (其他的幾面牆,則放入另一個串列 C2)。如此一來,我們可以讓 T 以類似深度優先 (depth-first) 搜尋的方式向外延伸,而能夠相對容易地增加 T 的高度。
那麼,如果 T 已經「碰到絕處」,無法用深度優先搜尋繼續往下增長時,該怎麼辦呢?此時,我們可以由 C2 取出最後面的牆來打破。如此持續進行,直到 C 與 C2 都是空集合為止。(喔,只是稍微修改 8 月 25 日 post 的「基本演算法」,產生出來的結果,竟然就會有如此大的差異...)
我想,或許迷宮真的是一個不錯的主題吧(連 MPH 從前也曾嘗試用「笨方法」產生曲折迷宮呢)。而回顧這些曾感興趣的問題,總讓我對從前懵懂的歲月,有著淡淡的感傷、歡喜與寂寞。
星期二, 9月 06, 2005
稍微有些曲折的迷宮
說過自己打算用「迷宮」來起頭,寫寫技術性文章。
也曾討論過,用 tree 來表示迷宮是一種頗為簡單、漂亮的作法。但是,從幾個產生的迷宮路徑圖來看(參考 8 月 15 日的 post),這種簡單方法所產生的迷宮「不夠蜿蜒曲折」。於是,就會想:如何才能產生比較蜿蜒曲折的迷宮呢?
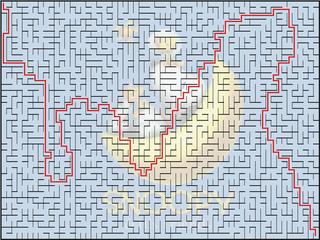 一種想法是,產生迷宮時(參考 8 月 25 日的 post),讓「候選集合 C」裡,每道「可被打破的牆」被打破的機率都不一樣。不過,問題是:該用怎樣的機率分配(該如何指定每道牆被選到、被打破的機率),才能得到蜿蜒的迷宮路徑呢?到目前為止,我試了幾種簡單的機率產生方式,但對結果都不甚滿意(有沒有人可以提供建議啊?)。
一種想法是,產生迷宮時(參考 8 月 25 日的 post),讓「候選集合 C」裡,每道「可被打破的牆」被打破的機率都不一樣。不過,問題是:該用怎樣的機率分配(該如何指定每道牆被選到、被打破的機率),才能得到蜿蜒的迷宮路徑呢?到目前為止,我試了幾種簡單的機率產生方式,但對結果都不甚滿意(有沒有人可以提供建議啊?)。
換一個角度思考:我們可以觀察到,從左上到右下的路徑,必得經過中間每一直行。因此,或許可嘗試另一種方式:在迷宮中,隨意產生幾道「長長的、不可被打破的牆」,強迫從左上到右下的路徑必得「繞路」。例如,右上方的迷宮,第 10 行與第 26 行右側各有一道由上往下的長牆,第 14 行右側有一道由下往上的長牆。如此一來,產生的迷宮似乎就蜿蜒曲折了些。
我覺得,可以有「激發想法、並修改程式來實驗改進」的餘地,也是迷宮問題的有趣地方。
也曾討論過,用 tree 來表示迷宮是一種頗為簡單、漂亮的作法。但是,從幾個產生的迷宮路徑圖來看(參考 8 月 15 日的 post),這種簡單方法所產生的迷宮「不夠蜿蜒曲折」。於是,就會想:如何才能產生比較蜿蜒曲折的迷宮呢?
 一種想法是,產生迷宮時(參考 8 月 25 日的 post),讓「候選集合 C」裡,每道「可被打破的牆」被打破的機率都不一樣。不過,問題是:該用怎樣的機率分配(該如何指定每道牆被選到、被打破的機率),才能得到蜿蜒的迷宮路徑呢?到目前為止,我試了幾種簡單的機率產生方式,但對結果都不甚滿意(有沒有人可以提供建議啊?)。
一種想法是,產生迷宮時(參考 8 月 25 日的 post),讓「候選集合 C」裡,每道「可被打破的牆」被打破的機率都不一樣。不過,問題是:該用怎樣的機率分配(該如何指定每道牆被選到、被打破的機率),才能得到蜿蜒的迷宮路徑呢?到目前為止,我試了幾種簡單的機率產生方式,但對結果都不甚滿意(有沒有人可以提供建議啊?)。換一個角度思考:我們可以觀察到,從左上到右下的路徑,必得經過中間每一直行。因此,或許可嘗試另一種方式:在迷宮中,隨意產生幾道「長長的、不可被打破的牆」,強迫從左上到右下的路徑必得「繞路」。例如,右上方的迷宮,第 10 行與第 26 行右側各有一道由上往下的長牆,第 14 行右側有一道由下往上的長牆。如此一來,產生的迷宮似乎就蜿蜒曲折了些。
我覺得,可以有「激發想法、並修改程式來實驗改進」的餘地,也是迷宮問題的有趣地方。
星期五, 9月 02, 2005
不用上班的一個星期
一般說來,「不用上班」似乎是「不用工作」的意思,是「悠閒」的代名詞。
不過,就如同 MPH 幾天前在 Blog 所言,不用上班的日子,感覺似乎更為忙碌(有時,我連早上看紐約時報的時間都不夠呢)。難道真的應驗了:「休息是為了更忙?」
我不清楚。我只知道,這幾天在家,倒是處理了許多上班時「忙碌而沒有做」的事情。通常,這類的事情必須麻煩家人來處理(所以啊,從前能夠空出一些時間,多少需要感謝家人的幫忙);而現在不用上班,就「理所當然」地該由自己來做了。
在家裡,似乎比較無法專心整理、回想、思考曾經感到興趣的電腦相關問題。因此,我會擔心:做這些「雜務事」,讓自己沒有什麼時間可以進行原先想進行的「心得、感想整理」。做這些事情,需要相當的專注、耐心、與毅力才能達成。
我希望,這幾天的忙碌,能夠算是「特例」。逐漸處理完「從前累積下來的事務」後,期待可以慢慢地「進入狀況」。
不過,就如同 MPH 幾天前在 Blog 所言,不用上班的日子,感覺似乎更為忙碌(有時,我連早上看紐約時報的時間都不夠呢)。難道真的應驗了:「休息是為了更忙?」
我不清楚。我只知道,這幾天在家,倒是處理了許多上班時「忙碌而沒有做」的事情。通常,這類的事情必須麻煩家人來處理(所以啊,從前能夠空出一些時間,多少需要感謝家人的幫忙);而現在不用上班,就「理所當然」地該由自己來做了。
在家裡,似乎比較無法專心整理、回想、思考曾經感到興趣的電腦相關問題。因此,我會擔心:做這些「雜務事」,讓自己沒有什麼時間可以進行原先想進行的「心得、感想整理」。做這些事情,需要相當的專注、耐心、與毅力才能達成。
我希望,這幾天的忙碌,能夠算是「特例」。逐漸處理完「從前累積下來的事務」後,期待可以慢慢地「進入狀況」。
訂閱:
意見 (Atom)