AB-game

雖然不知道 AB-game 的正式名稱，但我猜想，很多人都曾玩過類似的遊戲。

它是一種兩個人玩的遊戲：甲乙兩人各自在心裡想一個四位數字 (4 digits)，然後輪流讓方猜測這個數字（而自己則對此猜測的數字，依下一段的說明做回應）；能夠先猜出對方數字的人就算是贏家。

對於對方的猜測，回答的規則是這樣的：假設自己設想的數字是 a₃a₂a₁a₀（四位數字，在此千位數為 a₃，百位數為 a₂，十位數為 a₁，個位數為 a₀）而對方猜測的數字是 b₃b₂b₁b₀。若 x 為集合 {i | a_i=a_i} 的個數 (cardinality)，而令 y 代表集合 {i | a_i=b_j, i ≠ j} 的個數，則我們的回答就是 xAyB。

換句話說，x 是「數字相同、位置也相同」的個數，y 是「數字相同、但位置不同」的個數。例如，若設想的數字是 1234，而對方猜測 3614，則我們回答 1A2B（數字 4 出現的位置相同；而數字 1、3 出現的位置不同）；若設想的是 1357，對方猜 7890，則回答是 0A1B （沒有數字出現在相同的位置上；而有一個數字 7 出現在不同的位置）。

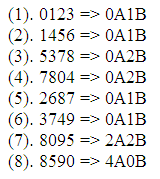在 AB-game 裡，我們通常會要求猜想的四位數字不可重覆；也就是說，要求 a_i≠a_j (i ≠ j)。至於第一位（千位數）a₃，一般則可以為零。因此，可猜想的數字，共有 10 x 9 x 8 x 7 = 5040 種可能。

右圖是一個可能的猜測序列。乙所選定的數字為 8590，而甲的運氣不太好：他先猜 0123，得到回答 0A1B；接著猜 1456，又得到一樣的回答 0A1B；如此這般，甲總共花了八個步驟，才猜對 8590 這個數字。

花了這麼多篇幅介紹這個遊戲，我到底想說些什麼？

我想說的，是一段聽聞與經驗有些衝突，但沒有經過驗證 (prove or disprove) 的情事：印象中，似乎曾聽人說過，「最糟的狀況，也僅需猜六次」。然而，在我的記憶裡，雖然在大多數情況下，的確只需要猜六次，但我似乎也曾有要猜七次（或七次以上）的經驗。

所以，為什麼只需要猜六次，就可以得到答案呢？