三談 AB-game

網路檢索到 Mastermind 相關的文章後，發現 Knuth 的方法確實可以減少猜測的次數。

我們或可將它視為一種「如何縮小可能性空間之優化處理」的方法。在先前「再談 AB-game」這篇 post 裡，提到甲每猜測一次，就可以藉由乙的回答，從「可能性空間」裡，刪除一些「不可能是答案」的數字。問題是，該猜測那個數字，才能夠排除最多不可能的答案呢？

Knuth 建議，選一個數字，讓「剩下的狀況裡，有最多可能性」的值是最小的 (choosing at every stage a test pattern that minimizes the maximum number of remaining possibilities)。

令人困擾的是，雖然 min(max(...)) 這樣的抽象式子簡潔漂亮，但是對於我這樣非數學系背景的人，通常並無法從這樣的式子中、看出它的直觀意義。因此，對這個式子多加些解釋，應該是有助於理解的。

對於目前的「可能性空間」（也就是「不會與乙對甲先前的猜測所給的回答」衝突的所有可能答案）而言，任何甲的新猜測都可能有 14 種回答（4A0B、2A2B、1A3B、0A4B、3A0B、2A1B、1A2B、0A3B、2A0B、1A1B、0A2B、1A0B、0A1B、0A0B -- 不可能有 3A1B 的情況發生）。這 14 種回答，可以將「目前的可能性空間」切割 (partition) 成 14 個集合。

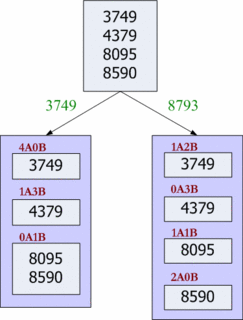例如，假設目前的可能性空間為 S = {3749, 4379, 8095, 8590}（參考右圖），若下一步甲猜 3749，則乙只可能有三種回答：4A0B（若乙的謎底也是 3749）、1A3B（若謎底為 4379）、或者 0A1B（謎底為 8095 或 8590）；其他像是 1A3B、0A4B 等等回答，都是不可能的。因此，3749 這個猜測，可以將 S 分割為 {3749}、{4379}、{8095, 8590}。

換個角度看，這樣的切割表示，經過甲的 3749 猜測後，可能性空間只能是 {3749}、{4379}、{8095, 8590} 這幾個分割中的一個。於是，我們知道：經過猜測 3749 這個數字後，「最大的可能性空間」是 {8095, 8590}，而其集合的個數 (cardinality) 則為 2。

值得提醒的是，我們不見得一定要猜測可能性空間裡的數字。例如，我們可以猜 8793，它可以將 S 切分為四個 cardinality 為 1 的 partitions：回答 1A1B 的 partition 為 {8095}、回答 2A0B 的 partition 為 {8590}、0A3B 的 {4379}、以及 1A2B 的 {3749}。

Kunth 的方法，就是從所有可能的新猜測裡，選擇會讓「最大可能性空間」個數 (cardinality) 為最小的那個數字。在上面的例子中，猜測 8793 會比猜測 3749 來得好；因為前者切分出的 partitions 中，最大的 cardinality 為 1；而後者切分後，最大的 cardinality 為 2。

我也依照這個演算法實作了程式。實際跑過後，它驗證了這個演算法，對於 Mastermind 的確可以在五步內猜得答案。然而，對於 AB-game，這個演算法卻仍然可能需要猜測七次。

所以，Knuth 的演算法，並不能證明「AB-game 在最壞的狀況下，也僅需要猜 6 次」的傳說（除非我程式寫錯啦，但這也並非不可能）。那麼，這個傳言的內容，究竟是真還是假呢？