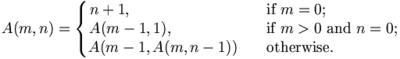我對 Ackermann's function （艾克曼函數）一直有著強烈的崇敬感。
讓我們先從兩個簡單的函數看起。如果 f(n) = n
n，那麼 f(0) = 1, f(1) = 1, f(2) = 2
2, f(3) = 3
3, ..., 它增長的速率是相當快的（也就是說，f(n+1) 會比 f(n) 的值要大上大頗多）。而如果 g(n) = n
n...n（共有 n 項），我們應該會對 g(n) 的增長速率感到些許敬畏、感到有些「遙不可及」。
可以想像，應該會有增長速率更快的函數。例如，Knuth 就曾提出一種
big-number（很大的數目）的表示法（注意到，這套表示法會用到無限多個（^, ^^, ^^^, ... ）運算子；而且這些運算子都是右結合（right associative）的，例如 2
34 = 2
(34) = 2
81）：
m ^ n = m m ... m (n 項) = m n
m^^n = m^m^...^m (n 項) = mm...m
m^^^n = m^^m^^...^^m (n 項)
Ackermann's function 的定義很簡單：
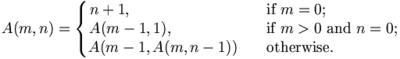
它簡單到用程式實作，幾乎只要照著定義抄就可以了。例如，以下就是一個用 PHP 實作的程式，它可以算出 A(3, 6) = 509：
<?php
function A($m, $n) {
if ($m == 0) return ($n + 1);
else {
if ($n == 0) return A($m-1, 1);
else return A($m-1, A($m, $n-1));
}
}
print "A(3, 6) = " . A(3, 6);
?>
令人驚訝的是，Ackermann's function 增長的速度非常快。現在的電腦威力已經很強了，但是要計算 A(4, 2) --- 更不用說是計算 A(5, 1) 了 --- 都還是會出現 Stack Overflow 或者 Out Of Memory 的錯誤訊息。事實上，Ackermann's function 增長的速度，比
m^n、
m^^n、甚至
m^^^n 都還要快。在數學上，它是一個 total recursive（全然迴歸：對於每個自然數 m, n，A(m, n) 都有定義）的函數，但是卻不是一個
primitive recursive（基本迴歸）函數。它增長的速度，遠超過一般人所能想像。
這也沒什麼嘛，數學的世界裡，本來就有許多令人驚詫的函數或定理，不是嗎？
是這樣的。十餘年前修習數理邏輯時，老師把「證明 Ackermann's function 非 primitive recursive」當成作業給學生做。那位老師 (Dr. Kueker) 很有趣，習題做錯後，他會點出錯誤所在（有時還會給一點提示），然後學生可以在學期內任何時刻再補交（如果還是做錯，可以下回再繼續補交）。重點是，這題我「證明」了三次，但每次都是錯的。一直到學期末，我想破了頭，都沒有證明出來。
也因為曾經努力數個月卻還是失敗，我對 Ackermann's function 一直有著頗為複雜的情感。有時，我會覺得：人就是這樣，對於盡力後依然失敗的情事，日後反而會留下最深刻的印象。
看看氣象預報，接下來一整個星期氣溫都會偏低，昨天算是不錯的天氣。想了想，淡水不好停車，還是開到左岸八里，坐渡船到淡水，走走逛逛好了。
經過了這許多年，似乎沒有太多人注意到這個問題，而更正版也沒有修正。或許，因為這本書的主旨是在「Complexity」，不是在「Logic」，所以很少人在意吧。
參考上圖，帶黑帽標示為小寫 b，戴白帽則標示為小寫 w。
有人說，實際是理論的延伸；也有人認為，理論是實際的抽象表達。那些聰明又有名氣的思想家，不管是支持哪一種論點，都能產生許多「有用」或「影響深遠」的思想或學說。
幾天前，曾提到「傳教士與食人族」的問題。
奇怪的是，我發現一個「違反直觀」的現象：調整「讓迷宮多轉些彎」的參數後，若「多轉彎」的機率大於「走直線」的機率，迷宮怎麼反而看起來更少曲折？（例如，右邊的兩張迷宮圖，路徑都頗「迂迴」，但下方的迷宮就比上方的迷宮有較多的轉彎。）
例如，假設目前的可能性空間為 S = {3749, 4379, 8095, 8590}（參考右圖），若下一步甲猜 3749，則乙只可能有三種回答：4A0B（若乙的謎底也是 3749）、1A3B（若謎底為 4379）、或者 0A1B（謎底為 8095 或 8590）；其他像是 1A3B、0A4B 等等回答，都是不可能的。因此，3749 這個猜測，可以將 S 分割為 {3749}、{4379}、{8095, 8590}。
事實上，我接觸到 Mastermind 這遊戲的時間，比 AB-game 還要早。印象中，大約在二十年前，大姊就曾買過這個益智遊戲來給家人玩了。
在 AB-game 裡，我們通常會要求猜想的四位數字不可重覆；也就是說，要求 ai≠aj (i ≠ j)。至於第一位（千位數）a3，一般則可以為零。因此，可猜想的數字，共有 10 x 9 x 8 x 7 = 5040 種可能。
例如，士林有一座國立科學教育館，假日人潮洶湧，但上班日通常門可羅雀，非常適合帶小朋友去走走。更棒的是，即使不買門票，也常能得到許多樂趣。
說的也是。既然手頭有程式，當然應該試著修改參數、做些實驗，看看會有怎樣不同的結果？
昨晚花了些時間，修改程式來做些實驗。終於，我們可以產生像右圖般的迷宮了。它看起來比昨天的迷宮，就蜿蜒曲折了許多（雖然我們也還是沒有定義出什麼叫做「蜿蜒曲折」）。
一種想法是，產生迷宮時（參考 8 月 25 日的 post），讓「候選集合 C」裡，每道「可被打破的牆」被打破的機率都不一樣。不過，問題是：該用怎樣的機率分配（該如何指定每道牆被選到、被打破的機率），才能得到蜿蜒的迷宮路徑呢？到目前為止，我試了幾種簡單的機率產生方式，但對結果都不甚滿意（有沒有人可以提供建議啊？）。
首先，假設我們要產生一個 3x3 的小迷宮。為了方便說明，我們將迷宮的格子標上號碼（英文字母 A~I），如右圖 (a) 所示。現在，且讓我們跟著演算法的步驟走一回：
它簡單到用程式實作，幾乎只要照著定義抄就可以了。例如，以下就是一個用 PHP 實作的程式，它可以算出 A(3, 6) = 509：
雖然我猜想，應該有「直觀、漂亮、簡單」的演算法可以產生蜿蜒的迷宮。例如，或許可以嘗試讓迷宮的樹狀結構長得深一些，這樣就可以拉長迷宮的「直徑」（迷宮 中，最長的兩個節點距離），而或許路徑就會顯得比較迂迴曲折。但是，在沒有合適的模型來定義「蜿蜒曲折」、或者在還沒有實際的實驗觀察前，我現在就是不知道答案。
